π Sayısını Hesaplama Algoritmaları

Bailey-Borwein-Plouffe (BBP) formülü

Bailey-Borwein-Plouffe (BBP) formülü, önceki haneleri hesaplamadan pi’nin (veya herhangi bir tabanda diğer sayıların) n’inci onaltılık hanesini hesaplamak için kullanılan bir formüldür. Formül, Simon Plouffe tarafından 1995 yılında keşfedilmiş olup, Peter Borwein ve Simon Plouffe’nin daha önceki çalışmalarına dayanmaktadır ve ayrıca David Bailey, Peter Borwein ve Simon Plouffe tarafından bağımsız olarak bulunmuştur.

BBP formülü, pi’yi, her bir terimin bir rasyonel sayı ile çarpıldığı ve 16’nın üsleri içeren bir toplam olarak ifade eden hızla yakınsayan bir seridir. Formül şöyledir:

pi = sum(k=0 to infinity) 16^(-k) * [4/(8k+1) – 2/(8k+4) – 1/(8k+5) – 1/(8k+6)]

BBP formülü, hesaplanan hanelerin önceki haneleri hesaplama gereksinimini ortadan kaldırdığı için, pi’nin onaltılık hanelerini hesaplama konusunda çok etkili bir yöntemdir. Formül, diğer sayı tabanları için de 16’nın uygun üssünü kullanarak adapte edilebilir.

BBP formülü, yüksek hassasiyete sahip pi hesaplamanın verimli bir yöntemi gerektiren bilgisayar bilimi ve kriptografi gibi alanlarda birçok uygulama bulmuştur. Ancak, BBP formülü, pi’nin genel olarak hesaplanması için daha genel bir formül sağlamadığından, pi’nin çoğu bilimsel uygulamasında sınırlı pratik kullanıma sahiptir.

C dilinde yazılmış π sayısını hesaplayan program

Altaki programı https://www.onlinegdb.com/ sitesinde test edebilirsiniz


#include "stdio.h"
#include "stdlib.h"
#include "gmp.h"

mpz_t tmp1, tmp2, t5, t239, pows;
void actan(mpz_t res, unsigned long base, mpz_t pows)
{
	int i, neg = 1;
	mpz_tdiv_q_ui(res, pows, base);
	mpz_set(tmp1, res);
	for (i = 3; ; i += 2) {
		mpz_tdiv_q_ui(tmp1, tmp1, base * base);
		mpz_tdiv_q_ui(tmp2, tmp1, i);
		if (mpz_cmp_ui(tmp2, 0) == 0) break;
		if (neg) mpz_sub(res, res, tmp2);
		else	  mpz_add(res, res, tmp2);
		neg = !neg;
	}
}

char * get_digits(int n, size_t* len)
{
	mpz_ui_pow_ui(pows, 10, n + 20);

	actan(t5, 5, pows);
	mpz_mul_ui(t5, t5, 16);

	actan(t239, 239, pows);
	mpz_mul_ui(t239, t239, 4);

	mpz_sub(t5, t5, t239);
	mpz_ui_pow_ui(pows, 10, 20);
	mpz_tdiv_q(t5, t5, pows);

	*len = mpz_sizeinbase(t5, 10);
	return mpz_get_str(0, 0, t5);
}

int main(int c, char **v)
{
	unsigned long accu = 16384, done = 0;
	size_t got;
	char *s;

	mpz_init(tmp1);
	mpz_init(tmp2);
	mpz_init(t5);
	mpz_init(t239);
	mpz_init(pows);

	while (1) {
		s = get_digits(accu, &got);

		
		got -= 2; 
		while (s[got] == '0' || s[got] == '9') got--;

		printf("%.*s", (int)(got - done), s + done);
		free(s);

		done = got;
		accu *= 2;
	}

	return 0;
}

Amstrad CPC BASIC dilinde π sayısını hesaplayan Spigot Algortiması

Spigot algoritması, tüm önceki basamakları hesaplamadan pi sayısının basamaklarını birer birer hesaplamak için kullanılan bir yöntemdir. İlk olarak Stanley Rabinowitz ve Stan Wagon tarafından 1995 yılında önerilmiştir ve bir “musluk” veya “tap” fikrine dayanır, bu tap birer birer pi sayısının basamaklarını çıkarmak için kullanılabilir.

Algoritma aşağıdaki gibi çalışır:

  1. Algoritmanın durumunu temsil etmek için bir dizi değişkeni başlatın.
  2. Her bir pi basamağını tek tek hesaplayın, ilk basamaktan başlayarak.
  3. Yeni basamağı eklemek için önceki tüm basamakları sağa kaydırın.
  4. İstenilen sayıda basamağı hesaplamak için adımları 2-3 tekrarlayın.

Spigot algoritması, pi sayısı için seri kimlik ve yaklaşımlar kullanarak, her basamağı sadece tamsayı aritmetiği kullanarak hesaplayan bir yöntemdir. Temel fikir, pi’nin bir devam eden kesir genişlemesini kullanmaktır, bu genişleme şu şekilde yazılabilir:

pi = 3 + 1/(7 + 1/(15 + 1/(1 + 1/(292 + …))))

Bu devam eden kesir, her adımda sadece birkaç terim hesaplamayı gerektiren şekilde kullanılabilir. Anahtar fikir, bu devam eden kesirden birer birer pi sayısının basamaklarını hesaplamak için “musluk” veya “tap” kullanmaktır, böylece önceki tüm basamakları hesaplamak gerekmez.

Spigot algoritması, C, Python ve Java gibi çeşitli programlama dilleri ve ortamlarında uygulanmıştır. Algoritma, hesaplama karmaşıklığı ve algoritma ile hesaplanabilecek büyük sayıda basamaklar nedeniyle, bilgisayar donanımı ve yazılımının performansını test etmek için sıklıkla bir ölçüt olarak kullanılmaktadır.

Altaki BASIC dilinde yazılmış olan programı https://benchmarko.github.io/CPCBasic/index.html bu sitede deneybilirsiniz

10 REM Amstrad CPC464
20 n = 1000
21 pi2$=””
30 ln = int(10*n/3)+16
40 nd = 1
50 dim a(ln)
60 n9 = 0
70 pd = 0 : rem First pre-digit is a 0
80 rem
90 for j = 1 to ln
100 a(j-1) = 2 : rem Start wirh 2S
110 next j
120 rem
130 for j = 1 to n
140 q = 0
150 for i = ln to 1 step -1 : rem Work backwards
160 x = 10*a(i-1)+q*i
170 a(i-1) = x-(2*i-1)*int(x/(2*i-1)) : rem X – Int ( X / Y) * Y
180 q = int(x/(2*i-1))
190 next i
200 a(0) = q-10*int(q/10)
210 q = int(q/10)
220 if q = 9 then n9 = n9+1 : goto 420
230 if q 10 then goto 350 ‘ burada eşit işaretini kaldırın
240 rem Q == 10
250 d = pd+1 : gosub 480
260 if n9 <= 0 then goto 310
270 for k = 1 to n9
280 d = 0 : gosub 480
290 next k
300 rem End If
310 pd = 0
320 n9 = 0
330 goto 420
340 rem Q 10
350 d = pd : gosub 480
360 pd = q
370 if n9 = 0 then goto 420
380 for k = 1 to n9
390 d = 9 : gosub 480
400 next k
410 n9 = 0
420 next j
430 pi2$=pi2$+mid$(str$(d),2) ‘print str$(pd)
440 print pi2$
450 end
460 rem
470 rem Output digits
480 if nd=0 then pi2$=pi2$+mid$(str$(d),2):return
500 if d = 0 then return
510 pi2$=pi2$+str$(d)+”.”
520 nd = 0
530 return

Program tarafından hesaplanan Pi 1000 basamak
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132000568127145263560827785771342757789609173637178721468440901224953430146549585371050792279689258923542019956112129021960864034418159813629774771309960518707211349999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420199

Full Precision Calculator sonucu

https://www.mathsisfun.com/calculator-precision.html


3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132000568127145263560827785771342757789609173637178721468440901224953430146549585371050792279689258923542019956112129021960864034418159813629774771309960518707211349999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420199

François Viète’nin pi sayısı için formülü

“François Viète’nin pi sayısı için formülü” olarak bahsettiğinizi düşünüyorum. François Viète, 16. yüzyılda yaşamış bir Fransız matematikçidir ve pi sayısının yaklaşık bir değerini hesaplamak için bir formül keşfetmiştir.

Bu formül, iç içe geçmiş köklerin oranlarının sonsuz bir çarpımına dayanır ve şöyle yazılabilir:

π = 2 × (2/√2) × (2/√(2+√2)) × (2/√(2+√(2+√2))) × …

Bu formül, sonsuz bir çarpımın bir örneğidir ve ilk n terimini çarparak pi’yi yüksek bir doğruluk derecesine kadar hesaplamak için kullanılabilir. Ancak, çok yavaş bir şekilde yakınsar, bu nedenle iyi bir yaklaşım elde etmek için birçok terim gereklidir.

Değerlendirme yapmak için Viète’nin formülünden daha verimli olan birçok başka algoritma bulunması da dikkat çekicidir.

C, Octave, Basic dillerinde LambertW fonksiyonu

Lambert W fonksiyonu (aynı zamanda omega fonksiyonu olarak da bilinir), matematikte özellikle karmaşık analiz ve ilgili alanlarda kullanılan özel bir fonksiyondur. Fonksiyon, f(z) = z * e^z fonksiyonunun tersidir, yani w(z) fonksiyonu, w(z) * e^w(z) = z denklemini sağlayan fonksiyondur. W(z) olarak gösterilir.

Lambert W fonksiyonu, matematik, bilim ve mühendislik gibi çeşitli alanlarda kullanılır. Örneğin, x^a = b veya a^x = b gibi üstel denklemlerin çözümünde kullanılabilir. Ayrıca, istatistik mekaniği, termodinamik ve finansta da kullanılır.

Lambert W fonksiyonu, karmaşık değerli bir fonksiyondur ve sonsuz sayıda dalga sahiptir. Lambert W fonksiyonunun ana dalı, -1/e’den büyük veya eşit olan gerçek argümanlar için gerçek değerleri alır ve z > -1/e için tek bir değerli ters fonksiyona sahiptir. Diğer dallar karmaşık değerlidir ve ana dalın 2πi katları eklenerek elde edilir.

Lambert W fonksiyonu, MATLAB, Mathematica, Python ve R gibi birçok matematiksel yazılım paketinde ve programlama dilinde uygulanmıştır.

LambertW fonsiyonunun Amstrad CPC makinelerde de çalışabilecek BASiC dilinde yazılmış bir versiyonunu alta ki programda görebilirsiniz

10 INPUT X
20 W = X
30 WHILE ABS(W*EXP(W)-X)/X > 1E-8
40     W = W - (W*EXP(W)-X)/(EXP(W)*(W+1)-((W+2)*(W*EXP(W)-X))/((2*W+2)+W*EXP(W)))
50 WEND
60 PRINT W

Programı kendinizde şu linkte test edebilrisiniz https://benchmarko.github.io/CPCBasic/index.html

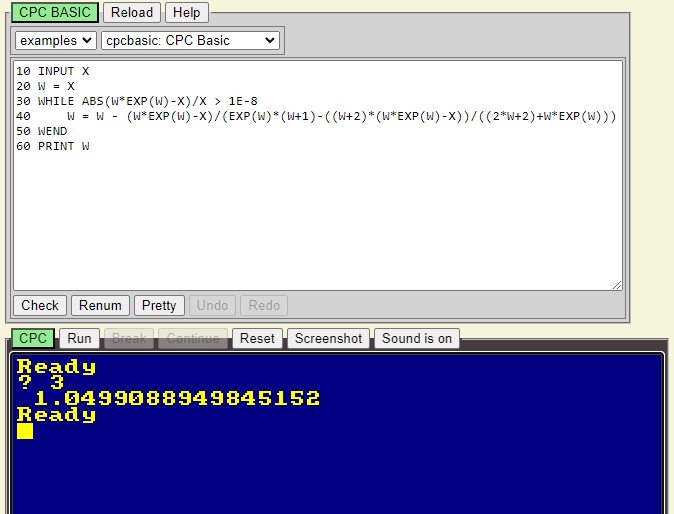
WolframAlpha da elde edilen sonuç ise

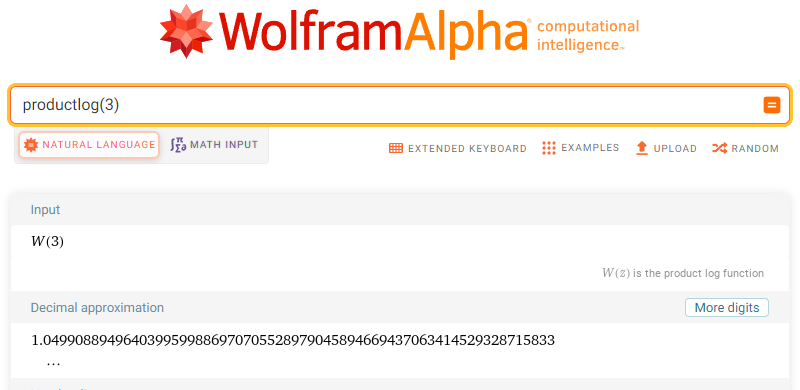
LambertW fonsiyonu aynı zamanda product log olarkata bilinir ve wolframalpha buadlandırmayı kullanıyor.

Sonuçları karşılaştıracak olursak BASİC ile yazılan program gayet iyi yakınsadıpını söyleyebiliriz

Programda şu değişiklikleri lgili satırda yaparsak

30 WHILE ABS(W*EXP(W)-X)/X > 1E-15

W(x)=1.04990889496404 noktadan sonra 14 basamak doğruğunda sonuç elde ederiz.

Dikkat edilmesi gereken husun x ler daima x>0 büyük olmalıdır. LambertW complex sayılar içinde tanımlı olsa da yazmış olduğumuz program sadece pozitif reel sayıların LambertW sunu hesaplayabilmektedir.

Örnek Porblem:

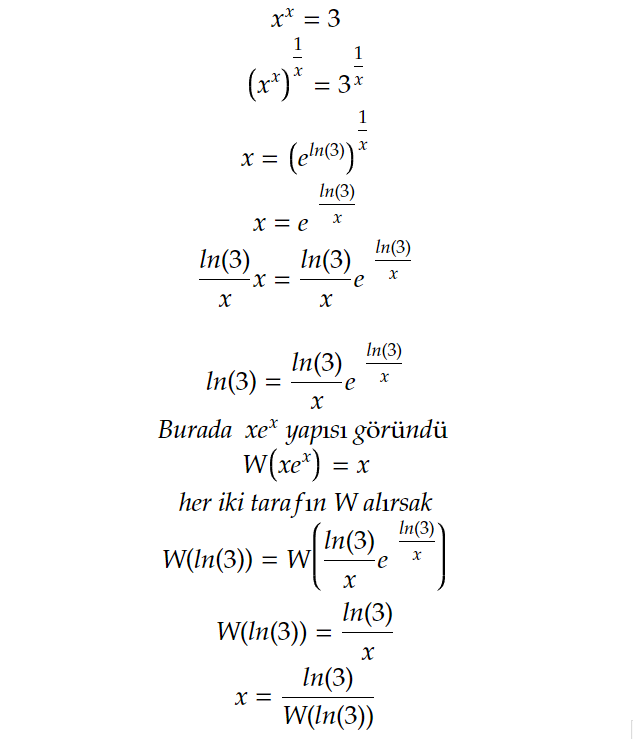
Şimdi W(ln(3)) programımıza hesaplatalım

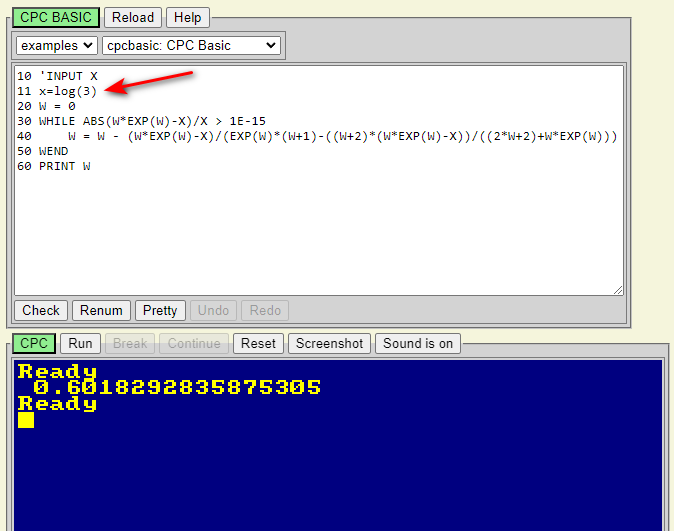
Amstrad’da

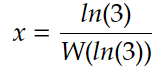
ifadesini hesaplatalım

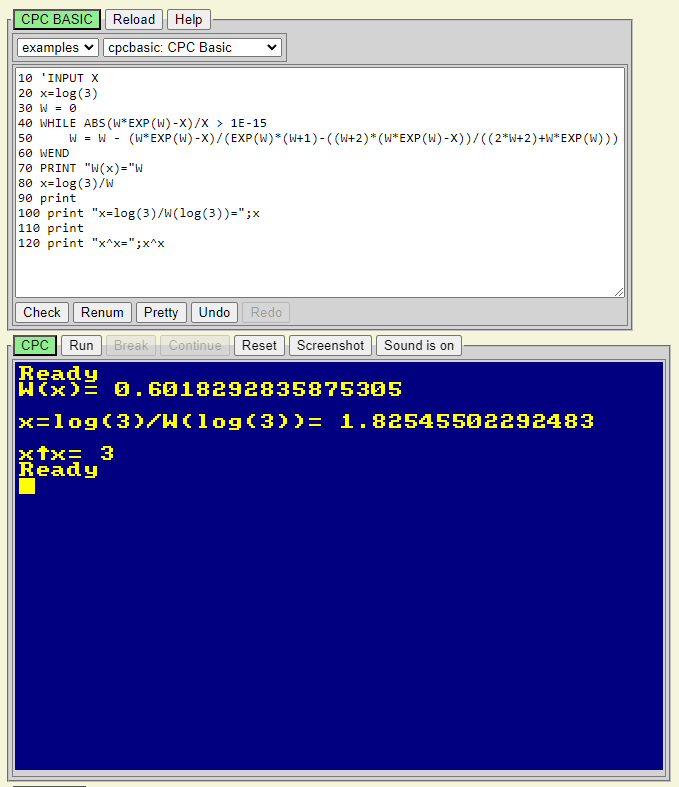
Görüldüğü üzere

W(log(3))=0.6018292835875305

x=1.82545502292483

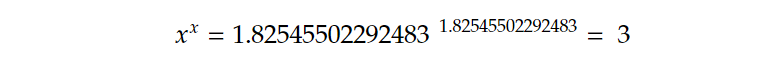
Sonuçtan da anlaşılacağı gibi AMSTRAD CPC464 için yazılan LambertW Basic porgramı sıfırdan büyük pozitif reel sayılar gayet düzgün çalışıyor ve doğru sonuç veriyor.

Örnekteki problemi çözen tam programın listesini aşağıda veriyorum

10 'INPUT X
20 x=LOG(3)
30 W=0
40 WHILE ABS(W*EXP(W)-X)/X>1E-15
50 W=W-(W*EXP(W)-X)/(EXP(W)*(W+1)-(W+2)*(W*EXP(W)-X)/(2*W+2+W*EXP(W)))
60 WEND
70 PRINT "W(x)="W
80 x=LOG(3)/W
90 PRINT
100 PRINT "x=log(3)/W(log(3))=";x
110 PRINT
120 PRINT "x^x=";x^x

Programı linkini https://benchmarko.github.io/CPCBasic/index.html online olan Amstrad simülatöründe deneyebilirsiniz

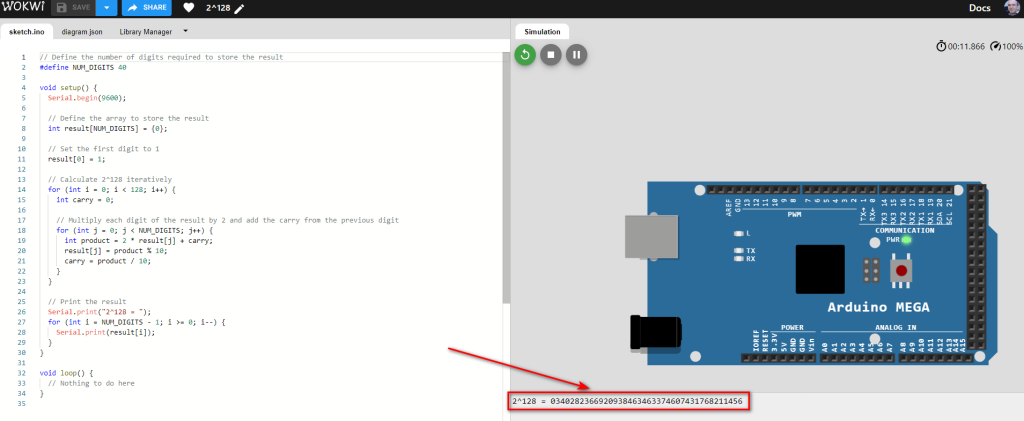
Bir sonraki macerada görüşmek üzere: C, Octave, Basic dillerinde LambertW fonksiyonu

Amstrad CPC bilgisayarı 2^128 hesaplıyor

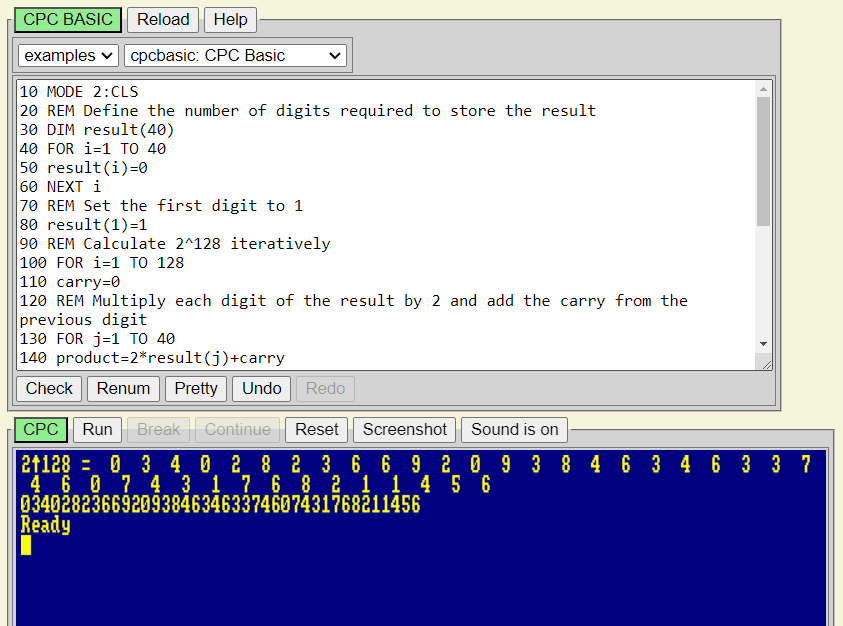
ChatGPT ye Arduino için yazdırdığım programı Amstrad Basic diline chatGPT ye çevrttim ancak bir hata yaptı onuda düzelttim satır 160 INT eklnmesi gerekiyordu. Ayıca sonucu daha düzgün görmek için satır 240-270 ekledim. Alta programı görebilrsiniz

10 MODE 2:CLS
20 REM Define the number of digits required to store the result
30 DIM result(40)
40 FOR i=1 TO 40
50 result(i)=0
60 NEXT i
70 REM Set the first digit to 1
80 result(1)=1
90 REM Calculate 2^128 iteratively
100 FOR i=1 TO 128
110 carry=0
120 REM Multiply each digit of the result by 2 and add the carry from the previous digit
130 FOR j=1 TO 40
140 product=2*result(j)+carry
150 result(j)=product MOD 10
160 carry=INT(product/10)
170 NEXT j
180 NEXT i
190 REM Print the result
200 PRINT "2^128 = ";
210 FOR i=40 TO 1 STEP -1
220 PRINT result(i);
230 NEXT i
240 FOR i=40 TO 1 STEP -1
250 res$=res$+MID$(STR$(result(i)),2)
260 NEXT i
270 PRINT res$

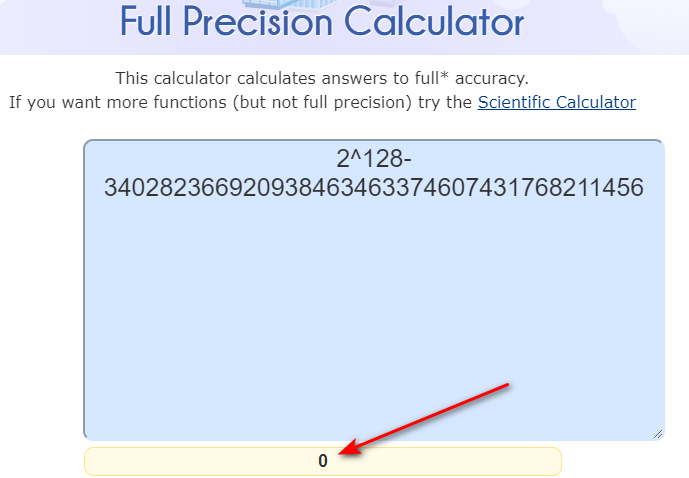
Sonucuda Amtrad mükemmel şekilde hesapladı.

Arduino ile 2^128 hesaplayan yazılımı ChatGPT ile beraber yazdık

// Define the number of digits required to store the result
#define NUM_DIGITS 40

void setup() {
  Serial.begin(9600);
  
  // Define the array to store the result
  int result[NUM_DIGITS] = {0};

  // Set the first digit to 1
  result[0] = 1;

  // Calculate 2^128 iteratively
  for (int i = 0; i < 128; i++) {
    int carry = 0;

    // Multiply each digit of the result by 2 and add the carry from the previous digit
    for (int j = 0; j = 0; i--) {
    Serial.print(result[i]);
  }
}

void loop() {
  // Nothing to do here
}

Wowki

https://wokwi.com/projects/361996755593355265

ChatGPT ile olan diyaloğumuz altaki resimde görülüyor

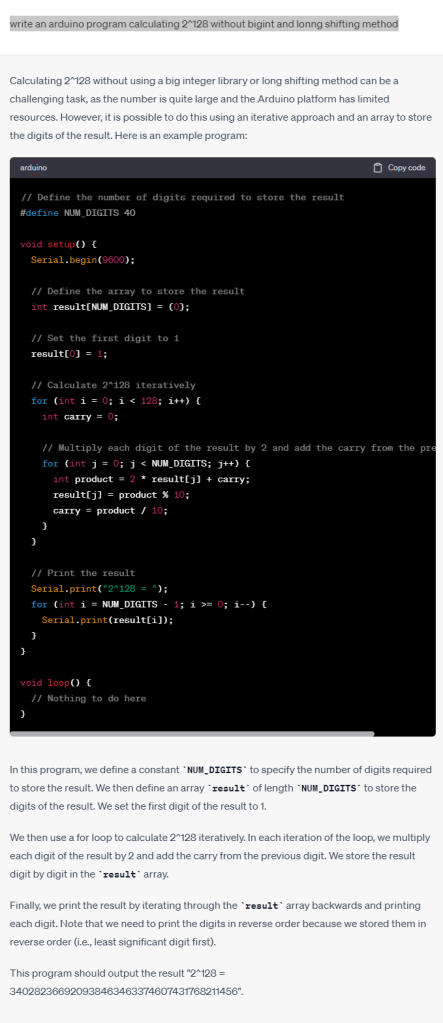
Arduino ile 100! hesaplayan kodu chatGPT ye yazdırdım

BU chatGPT ye aklıma gelen işkence vari arduino kodları yazdırmak bir takıntı haline geldi bazen uğraştırıyor bazen ne dediğini anlamıyor bazen sabrımı taşırıyor. Daha önceleri de yaptığım denemelerde epey hatalı kodlar üretiyordu. ChatGPT ye olabildiğince net talimatla rvermek gerekiyor ve doğru sonuç verme olasılığı artmış olur.

Bugün tekrar Arduino için 100! (faktoryel) kodunu yazmasın istedim.

Chat kutusuna “write a code for arduino calculating 100! without using bigINT library”

ve chatGPT’ nin yazdığı kod;

void setup() {
  Serial.begin(9600);   // Start serial communication
}

void loop() {
  int result[200];   // Array to store the digits of the factorial
  int n = 100;   // Calculate the factorial of 100
  int length = 1;   // Current length of the factorial

  // Initialize the array with 1 digit
  result[0] = 1;

  // Multiply the factorial by each number from 2 to n
  for (int i = 2; i <= n; i++) {
    int carry = 0;   // Carry from the previous multiplication

    // Multiply each digit of the factorial by i and add the carry
    for (int j = 0; j = 0; i--) {
    Serial.print(result[i]);
  }
  Serial.println();

  while(1);   // Stop the program
}

Bu programı wowki de, siz de bu altaki linkte deneybilirsiniz

https://wokwi.com/projects/361886801962539009

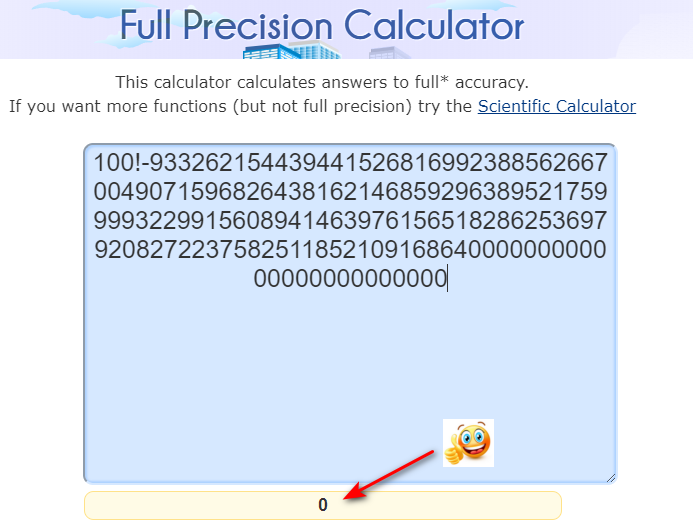
Ben çalıştırdım ve sonuç 

93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

Sonucu Full Precision Calculator ‘ da teyyit ettim sonuç mükemmel.

chatGPT gitgide kendini geliştiriyor. Daha zorlu kodlara geçme zamanı geldi. Yeni denemelere devam edeceğim takipte kalın.

ChaGPT Arduino’ da uzun bölme yapan program yazdı

void setup() {
   Serial.begin(9600);
}

void loop() {
   long dividend = 12345;
   long divisor = 123456;
   int decimal_places = 1000;
   
   char result[decimal_places+2]; // +2 for decimal point and null terminator
   memset(result, 0, sizeof(result)); // initialize result to all zeroes
   
   // Handle negative values
   bool negative = false;
   if ((dividend  0) || (dividend > 0 && divisor < 0)) {
     negative = true;
   }
   dividend = abs(dividend);
   divisor = abs(divisor);
   
   // Calculate integer part of quotient
   long quotient = dividend / divisor;
   ltoa(quotient, result, 10);
   
   // Add decimal point
   strcat(result, ".");
   
   // Calculate decimal part of quotient
   long remainder = dividend % divisor;
   for (int i = 0; i < decimal_places; i++) {
     remainder *= 10;
     quotient = remainder / divisor;
     remainder = remainder % divisor;
     result[i+2] = quotient + '0';
   }
   
   // Print result
   if (negative) {
     Serial.print("-");
   }
   Serial.println(result);
   
   while (1) {} // stop program from continuing indefinitely
}

ChaGPT kullanarak arduino ya program yazdırdım

ChatGPT ilk aktif olduğunda üye olup kullanmışlığım vardı. sadece iki sorudan oluşan bir muhabbet. Biri Aşkın tanımı nedir diğeri de Steve Jobs’ un Biyografisi hakkındaydı. Daha sonraları sistemin yoğunluğundan dolayı giriş yapamadım ve çok fazla deneme fırsatım olmadı hatta neler yapılabileceği konusunda da çok fikrim yoktu. Yine dedim bir zamanlar çok fonksiyonel olmayan yapay zeka ile Chat yazılımlarına benziyordur diye çok üstüne düşmedim. Son bir kaç haftadır youtube de sıkça videolar görmeye başladım. Merakımı tekrar celbetti. Hadi ChapGPT Arduino için bana bir yazılım yazmasını istedim . Blog da daha önce Amstrad bilgisayar için BASIC’ te yazılan bir programı ChatGPT’ nin Arduino için yazmasını istedim.

Çok büyük sayılar çarpımını yapabilecek bir Arduino programını yazması için chat kutusuna yazmaya başladım.

Continue reading ChaGPT kullanarak arduino ya program yazdırdım

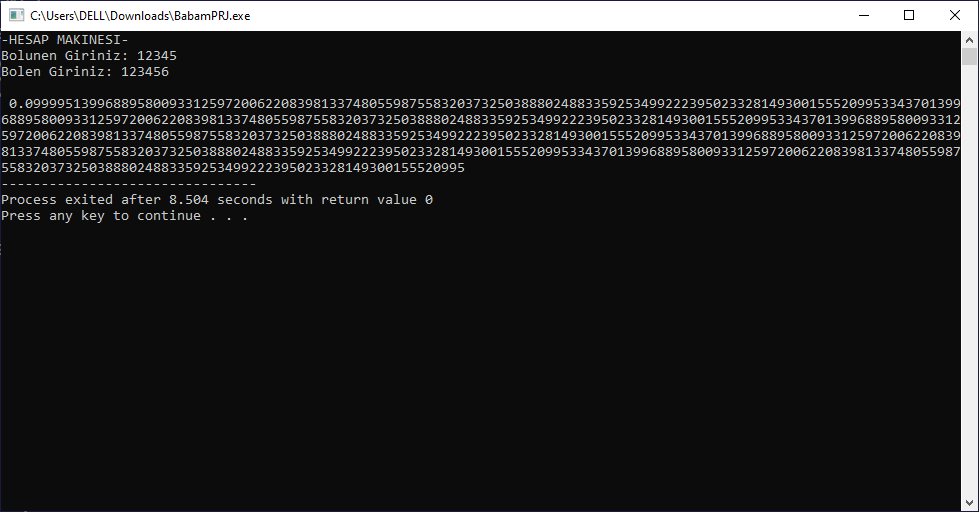
C programı ile Sonsuz Bölme

Bu program ile 2 sayının bölümünü virgülden sonra istediğiniz kadar hesaplatabilirsiniz. Aşağıdaki programı devC++ ile çalıştırabilirsiniz. Program virgülden sonra 1000 basamak hesaplamaktadır, istediğiniz taktirde programdan yapacağınız değişiklikle basamak sayısını arttırabilirsiniz.

#include 

int main(){
	int bnn,bln,sayac=0;
	printf("-HESAP MAKINESI-\n");
	printf("Bolunen Giriniz: ");
	scanf("%d",&bnn);
	printf("Bolen Giriniz: ");
	scanf("%d",&bln);
		
	float temp;
	printf("\n %d.",bnn/bln);
	bnn=bnn%bln;
	while(sayacbln){
			
			printf("%d",bnn/bln);
			bnn=bnn%bln;
			//printf(" -%d- ",bnn);
		}
		else{
			bnn*=10;
			if(bnn<bln){
				if(bnn%bln!=0){
					printf("0");
				}
			}
			//printf(" +%d+ ",bnn);
			if(bnn%bln==0 && !(bnn/bln!=0)){
				printf("0");
			}
		}
	}
}

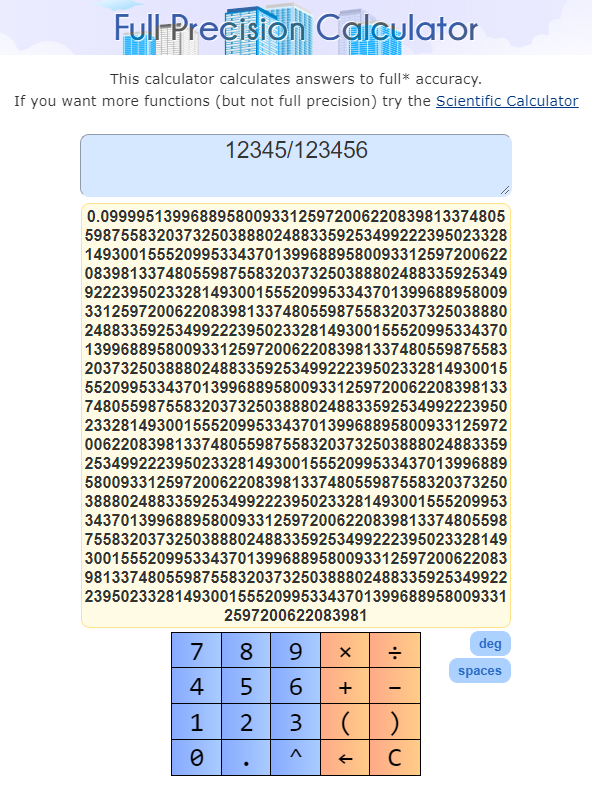
Buradaki bağlantıdan Full Precision Calculator’a erişebilirsiniz https://www.mathsisfun.com/calculator-precision.html.

Full Precision Calculator ile 1000 basamak hesaplatılmıştır. C programı ile karşılaştırmayı yapabilirsiniz.

Amstrad CPC ‘ler ile büyük sayıların çarpımı.

Amstrad CPC’ ler 8 bit olan Z80 mikroişlemcisi ile çalışmaktadır. Z80 nin keni içinde donanımsal çarpma işlemi yapan birime sahip değildir. Z80 8 biraz zorlarsak 16 bit toplama çıkarma 8 bit sağa sola kaydırma işlemleri yapabilmektedir. Tüm çarpma bölme algoritması yazılımsal olarak gerçekleştirilmektedir. Amstradların kendi ROM’ undaki ve Locomotif basic’ in kullandığı çarpa işlemininde sınırları vardır. Belli büyüklükte sayıların çarpımını artık tam sayı olarak değilde üstel olarak vermektedir. Amstrad ile çok büyük sayıların çarpımı yapacak BASiC dilinde yazılmış bir program buldum ve az bir düzenlmeyle Amtradlarda çalışır hale getirdim.

Aşağıda BASiC programı gerçek bir Amtsrad’ da veya herhangi bir Amstrad emülatörde deneyebilirsiniz. 

100 REM DEFDBL A-H 
110 REM
120 DIM A(1,31),B(63):H=100000000
130 CLS:
131 FOR I=0 TO 1:M=N:INPUT"* ";P$
132 L=LEN(P$):N= INT(L/8):A(I,N)=VAL(LEFT$(P$,(L MOD 8)))
140 FOR J=1 TO N:A(I,J-1)=VAL(MID$(P$,L-8*J+1,8)): NEXT J:NEXT I 
150 FOR I=0 TO M:E=A(0,I):FOR J=I TO I+N:F=B(J)+E* A(1,J-I)
160 G=INT(F/H):B(J+1)=B(J+1)+G:B(J)=F-G*H:NEXT J:NEXT I
180 PRINT:PRINT:L=M+N+(G=0):PRINT USING"**######";B(L+1);:FOR I=0 TO L 
200 PRINT SPC(-((I MOD 9)<8));RIGHT$(STR$(B(L-I)+H ),8);:NEXT I:END